偏差和方差是训练机器学习模型时要调整的核心参数。当讨论预测模型时，预测误差可以分解为两个主要的量：偏差引起的误差和方差引起的误差。

偏差-方差权衡是偏差引入的误差与方差产生的误差之间的张力 。为了了解如何充分利用这种权衡并避免欠拟合或过拟合我们的模型，让首先了解偏差是一种方差。

偏差引起的误差

偏差引起的误差是模型的预测值与真实值之间的距离。在这种类型的错误中，模型很少关注训练数据，过度简化了 模型。

由于差异而导致的错误

给定数据点的模型预测的可变性或告诉数据分布的值。在这种类型的错误中，模型在训练数据中投入了大量精力，以至于记住它而不是从中学习。具有高方差误差的模型无法灵活地对以前从未见过的数据进行泛化。

Bias — Variance 权衡

偏差 - 方差权衡是关于平衡和在偏差引起的误差和方差引起的误差之间找到一个最佳点。

这是一个 Underfitting 与 Overfit 的困境

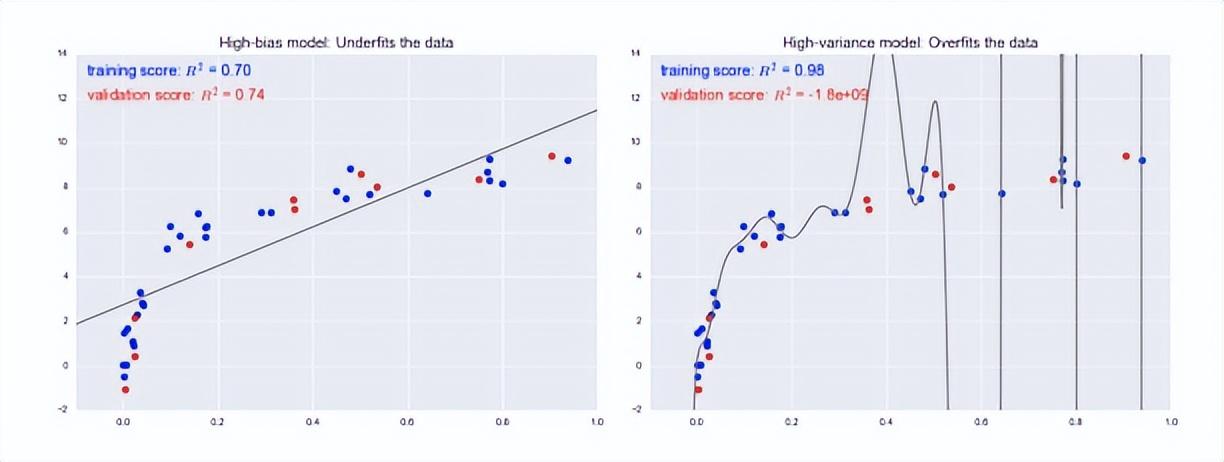
如果模型由灰色线表示可以看到高偏差模型是过度简化数据的模型，而高方差模型是过于复杂而过度拟合数据的模型。

总之：

• 偏差 是模型为使目标函数更易于近似而做出的简化假设。
• 方差 是给定不同训练数据的情况下，目标函数的估计值将发生变化的量。
• 偏差-方差权衡 是机器模型在偏差和方差引入的误差之间执行的最佳点。